本课程涵盖矢量微积分的理论基础和实际应用。第一周,学生将学习标量场和向量场。第二周,他们将对场进行微分。第三周的重点是多维积分和曲线坐标系。第四周学习线积分和面积分,第五周探索向量微积分的基本定理,包括梯度定理、发散定理和斯托克斯定理。这些定理对于电磁学和流体力学等工程学科目至关重要。 请注意,本课程在某些大学也可能被称为多元微积分或多元微积分或微积分 3。本课程的先决条件是学习过两个学期的单变量微积分(微分和积分)。 课程包括 53 个简明的讲座视频,每个视频后都有几个问题需要解决。每个主要课题之后都有一个简短的练习测验。每周结束时,都有一次评估测验。问题和练习测验的答案可在教师提供的讲义中找到。
即将结束: 只需 199 美元(原价 399 美元)即可通过 Coursera Plus 学习新技能。立即节省

了解顶级公司的员工如何掌握热门技能

积累特定领域的专业知识
- 向行业专家学习新概念
- 获得对主题或工具的基础理解
- 通过实践项目培养工作相关技能
- 获得可共享的职业证书

该课程共有5个模块
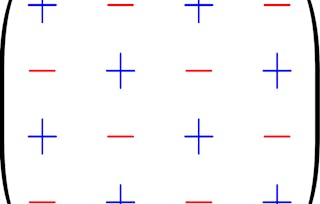
矢量是既有长度又有方向的数学构造。 我们将定义矢量,演示如何进行加减运算,以及如何使用点积和十字积进行乘法运算。 我们应用矢量来研究直线和平面的解析几何,并定义 Kronecker delta 和 Levi-Civita 符号来证明矢量等式。 最后,我们将定义标量场和向量场的重要概念。
涵盖的内容
15个视频27篇阅读材料5个作业2个插件
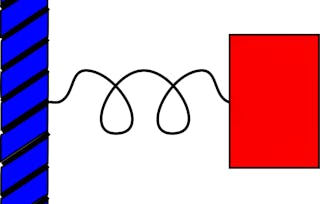
标量场和向量场都可以微分。 我们定义了偏导数,并将最小二乘法推导为最小化问题。 我们将学习如何对多个变量的函数使用链式法则,并推导出化学工程中使用的三乘法则。 我们定义了梯度、发散、卷曲和拉普拉斯。 我们学习一些有用的矢量微积分等式,并使用 Kronecker delta 和 Levi-Civita 符号推导它们。 我们利用矢量等式从麦克斯韦方程推导出自由空间中的电磁波方程。 电磁波是所有现代通信技术的基础。
涵盖的内容
13个视频15篇阅读材料4个作业
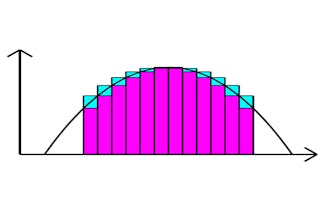
积分可以扩展到多个变量的函数。 我们将学习如何进行二重积分和三重积分。 我们定义了曲线坐标,即二维的极坐标和三维的圆柱坐标和球面坐标,并用它们来简化具有圆、圆柱或球面对称性的问题。 我们将学习如何书写曲线坐标中的微分算子,以及如何使用变换的雅各布值来改变多维积分中的变量。
涵盖的内容
12个视频24篇阅读材料4个作业
标量场或向量场可以在曲线或曲面上积分。 我们将学习如何对标量场进行线积分,并利用线积分计算弧长。 然后,我们将学习如何通过求矢量场与曲线切线单位矢量的点积来求矢量场的线积分。 考虑力场的线积分可以得出功-能定理。 接下来,我们学习如何求标量场的表面积分,并利用表面积分计算表面积。 然后,我们学习如何通过求矢量场与表面法线单位矢量的点积来求矢量场的表面积分。 速度场的表面积分用于定义流体通过表面的质量通量。
涵盖的内容
9个视频11篇阅读材料3个作业
微积分基本定理将积分与微分联系起来。 在这里,我们将学习相关的向量微积分基本定理。 这些定理包括梯度定理、发散定理和斯托克斯定理。 我们将展示如何利用这些定理推导连续性方程和能量守恒定律。 我们将展示如何以无坐标形式定义发散和卷曲,以及如何将麦克斯韦方程组的积分形式转换为微分形式。
涵盖的内容
13个视频21篇阅读材料4个作业
获得职业证书
将此证书添加到您的 LinkedIn 个人资料、简历或履历中。在社交媒体和绩效考核中分享。
位教师

从 数学与逻辑 浏览更多内容
 状态:预览
状态:预览The Hong Kong University of Science and Technology
 状态:免费试用
状态:免费试用The Hong Kong University of Science and Technology
 状态:免费试用
状态:免费试用The Hong Kong University of Science and Technology
 状态:预览
状态:预览Korea Advanced Institute of Science and Technology(KAIST)
人们为什么选择 Coursera 来帮助自己实现职业发展




学生评论
1,399 条评论
- 5 stars
83.78%
- 4 stars
14%
- 3 stars
1.28%
- 2 stars
0.57%
- 1 star
0.35%
显示 3/1399 个
已于 May 24, 2020审阅
The course was very systematically designed. It gave us practice problems once the concept is covered. But 4th module was a bit tough. The professor taught it excellently.
已于 May 14, 2021审阅
Professor Chasnov is a great instructor. I strongly recommend this course (and others from his). Thank you so much for making such great quality content available for everyone no matter where.
已于 Jul 17, 2020审阅
It was great, the professor did a great job in explanation, but at the same time, he didn't explain further with examples for some topics which made it really challenging for me to understand.
常见问题
要获取课程资料、作业和证书,您需要在注册课程时购买证书体验。 您可以尝试免费试听,或申请资助。课程可能提供 "完整课程,无证书"。通过该选项,您可以查看所有课程资料,提交必要的评估,并获得最终成绩。这也意味着您无法购买证书体验。
注册课程后,您就可以访问专项课程中的所有课程,完成作业后还可以获得证书。您的电子证书将添加到您的 "成就 "页面--在那里,您可以打印证书或将其添加到您的 LinkedIn 个人资料中。
是的。在特定的学习课程中,如果您付不起注册费,可以申请助学金或奖学金。如果您选择的学习课程有助学金或奖学金,您可以在说明页面找到申请链接。
更多问题
提供助学金,




